Home

Contest: Task: Related: TaskA TaskC

Score : $200$ points

Problem Statement

AtCoDeer the deer found two rectangles lying on the table, each with height $1$ and width $W$. If we consider the surface of the desk as a two-dimensional plane, the first rectangle covers the vertical range of $[0,1]$ and the horizontal range of $[a,a+W]$, and the second rectangle covers the vertical range of $[1,2]$ and the horizontal range of $[b,b+W]$, as shown in the following figure:

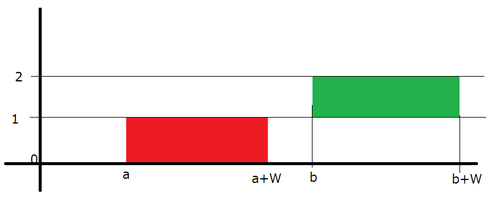
AtCoDeer will move the second rectangle horizontally so that it connects with the first rectangle. Find the minimum distance it needs to be moved.

Constraints

All input values are integers.
$1≤W≤10^5$
$1≤a,b≤10^5$

Input

The input is given from Standard Input in the following format:

$W$ $a$ $b$

Output

Print the minimum distance the second rectangle needs to be moved.

Sample Input 1

3 2 6

Sample Output 1

This input corresponds to the figure in the statement. In this case, the second rectangle should be moved to the left by a distance of $1$.

Sample Input 2

3 1 3

Sample Output 2

The rectangles are already connected, and thus no move is needed.

Sample Input 3

5 10 1