Home

Problem Statement

Snuke is conducting an optical experiment using mirrors and his new invention, the rifle of Mysterious Light.

Three mirrors of length $N$ are set so that they form an equilateral triangle. Let the vertices of the triangle be $a, b$ and $c$.

Inside the triangle, the rifle is placed at the point $p$ on segment $ab$ such that $ap = X$. (The size of the rifle is negligible.) Now, the rifle is about to fire a ray of Mysterious Light in the direction of $bc$.

The ray of Mysterious Light will travel in a straight line, and will be reflected by mirrors, in the same ways as "ordinary" light. There is one major difference, though: it will be also reflected by its own trajectory as if it is a mirror! When the ray comes back to the rifle, the ray will be absorbed.

The following image shows the ray's trajectory where $N = 5$ and $X = 2$.

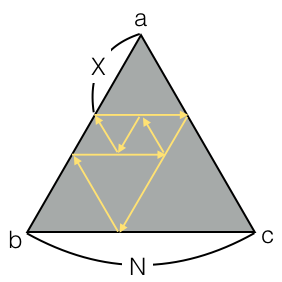
It can be shown that the ray eventually comes back to the rifle and is absorbed, regardless of the values of $N$ and $X$. Find the total length of the ray's trajectory.

Constraints

• $2≦N≦10^{12}$
• $1≦X≦N-1$
• $N$ and $X$ are integers.

Partial Points

• $300$ points will be awarded for passing the test set satisfying $N≦1000$.
• Another $200$ points will be awarded for passing the test set without additional constraints.

Sample Input 1

5 2

Sample Output 1

12

Refer to the image in the Problem Statement section. The total length of the trajectory is $2+3+2+2+1+1+1 = 12$.