Home

Problem Statement

Aoki loves numerical sequences and trees.

One day, Takahashi gave him an integer sequence of length $N$, $a_1, a_2, ..., a_N$, which made him want to construct a tree.

Aoki wants to construct a tree with $N$ vertices numbered $1$ through $N$, such that for each $i = 1,2,...,N$, the distance between vertex $i$ and the farthest vertex from it is $a_i$, assuming that the length of each edge is $1$.

Determine whether such a tree exists.

Constraints

• $2 ≦ N ≦ 100$
• $1 ≦ a_i ≦ N-1$

Sample Input 1

5
3 2 2 3 3

Sample Output 1

Possible

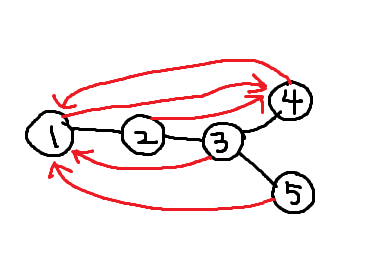
The diagram above shows an example of a tree that satisfies the conditions. The red arrows show paths from each vertex to the farthest vertex from it.

Sample Input 2

3
1 1 2

Sample Output 2

Impossible

Sample Input 3

10
1 2 2 2 2 2 2 2 2 2

Sample Output 3

Possible

Sample Input 4

10
1 1 2 2 2 2 2 2 2 2

Sample Output 4

Impossible

Sample Input 5

6
1 1 1 1 1 5

Sample Output 5

Impossible

Sample Input 6

5
4 3 2 3 4

Sample Output 6

Possible