Home
Contest: Task: Related: TaskA TaskC
Score : $400$ points
Problem Statement
We have a pyramid with $N$ steps, built with blocks. The steps are numbered $1$ through $N$ from top to bottom. For each $1≤i≤N$, step $i$ consists of $2i-1$ blocks aligned horizontally. The pyramid is built so that the blocks at the centers of the steps are aligned vertically.
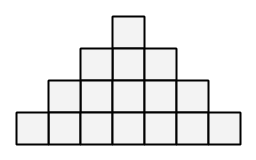
A pyramid with $N=4$ steps
Snuke wrote a permutation of ($1$, $2$, $...$, $2N-1$) into the blocks of step $N$. Then, he wrote integers into all remaining blocks, under the following rule:
- The integer written into a block $b$ must be equal to the median of the three integers written into the three blocks directly under $b$, or to the lower left or lower right of $b$.
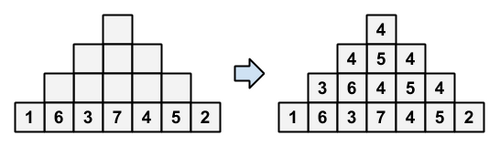
Writing integers into the blocks
Afterwards, he erased all integers written into the blocks. Now, he only remembers that the integer written into the block of step $1$ was $x$.
Construct a permutation of ($1$, $2$, $...$, $2N-1$) that could have been written into the blocks of step $N$, or declare that Snuke's memory is incorrect and such a permutation does not exist.
Constraints
- $2≤N≤10^5$
- $1≤x≤2N-1$
Input
The input is given from Standard Input in the following format:
$N$ $x$
Output
If no permutation of ($1$, $2$, $...$, $2N-1$) could have been written into the blocks of step $N$, print No.
Otherwise, print Yes in the first line, then print $2N-1$ lines in addition.
The $i$-th of these $2N-1$ lines should contain the $i$-th element of a possible permutation.
Sample Input 1
4 4
Sample Output 1
Yes 1 6 3 7 4 5 2
This case corresponds to the figure in the problem statement.
Sample Input 2
2 1
Sample Output 2
No
No matter what permutation was written into the blocks of step $N$, the integer written into the block of step $1$ would be $2$.