Home

Contest: Task: Related: TaskB TaskD

Score : $800$ points

Problem Statement

Takahashi has received an undirected graph with $N$ vertices, numbered $1$, $2$, ..., $N$. The edges in this graph are represented by $(u_i, v_i)$. There are no self-loops and multiple edges in this graph.

Based on this graph, Takahashi is now constructing a new graph with $N^2$ vertices, where each vertex is labeled with a pair of integers $(a, b)$ ($1 \leq a \leq N$, $1 \leq b \leq N$). The edges in this new graph are generated by the following rule:

Span an edge between vertices $(a, b)$ and $(a', b')$ if and only if both of the following two edges exist in the original graph: an edge between vertices $a$ and $a'$, and an edge between vertices $b$ and $b'$.

How many connected components are there in this new graph?

Constraints

$2 \leq N \leq 100,000$
$0 \leq M \leq 200,000$
$1 \leq u_i < v_i \leq N$
There exists no pair of distinct integers $i$ and $j$ such that $u_i = u_j$ and $v_i = v_j$.

Input

The input is given from Standard Input in the following format:

$N$ $M$
$u_1$ $v_1$
$u_2$ $v_2$
:
$u_M$ $v_M$

Output

Print the number of the connected components in the graph constructed by Takahashi.

Sample Input 1

3 1
1 2

Sample Output 1

The graph constructed by Takahashi is as follows.

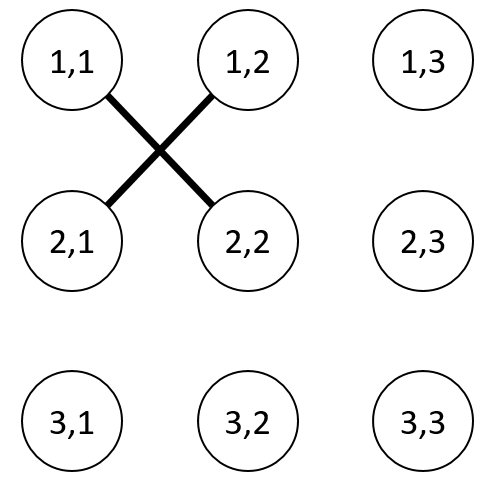
Sample Input 2