Home

Problem Statement

Joisino has a bar of length $N$, which has $M$ marks on it. The distance from the left end of the bar to the $i$-th mark is $X_i$.

She will place several squares on this bar. Here, the following conditions must be met:

• Only squares with integral length sides can be placed.
• Each square must be placed so that its bottom side touches the bar.
• The bar must be completely covered by squares. That is, no square may stick out of the bar, and no part of the bar may be left uncovered.
• The boundary line of two squares may not be directly above a mark.

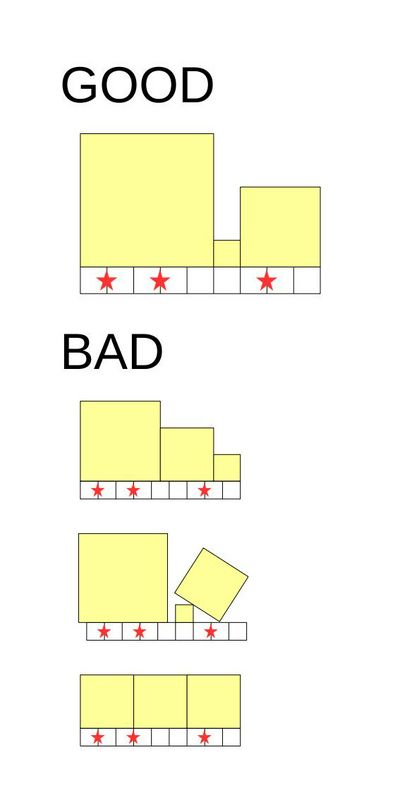
Examples of arrangements that satisfy/violate the conditions

The beauty of an arrangement of squares is defined as the product of the areas of all the squares placed. Joisino is interested in the sum of the beauty over all possible arrangements that satisfy the conditions. Write a program to find it. Since it can be extremely large, print the sum modulo $10^9+7$.

Constraints

• All input values are integers.
• $1 \leq N \leq 10^9$
• $0 \leq M \leq 10^5$
• $1 \leq X_1 < X_2 < ... < X_{M-1} < X_M \leq N-1$

Sample Input 1

3 1
2

Sample Output 1

13

There are two possible arrangements:

• Place a square of side length $1$ to the left, and place another square of side length $2$ to the right
• Place a square of side length $3$

The sum of the beauty of these arrangements is $(1 \times 1 \times 2 \times 2) + (3 \times 3) = 13$.

Sample Input 2

5 2
2 3

Sample Output 2

66

Sample Input 3

10 9
1 2 3 4 5 6 7 8 9

Sample Output 3

100

Sample Input 4

1000000000 0

Sample Output 4

693316425