Home

Problem Statement

Nuske has a grid with $N$ rows and $M$ columns of squares. The rows are numbered $1$ through $N$ from top to bottom, and the columns are numbered $1$ through $M$ from left to right. Each square in the grid is painted in either blue or white. If $S_{i,j}$ is $1$, the square at the $i$-th row and $j$-th column is blue; if $S_{i,j}$ is $0$, the square is white. For every pair of two blue square $a$ and $b$, there is at most one path that starts from $a$, repeatedly proceeds to an adjacent (side by side) blue square and finally reaches $b$, without traversing the same square more than once.

Phantom Thnook, Nuske's eternal rival, gives $Q$ queries to Nuske. The $i$-th query consists of four integers $x_{i,1}$, $y_{i,1}$, $x_{i,2}$ and $y_{i,2}$ and asks him the following: when the rectangular region of the grid bounded by (and including) the $x_{i,1}$-th row, $x_{i,2}$-th row, $y_{i,1}$-th column and $y_{i,2}$-th column is cut out, how many connected components consisting of blue squares there are in the region?

Process all the queries.

Constraints

• $1 ≤ N,M ≤ 2000$
• $1 ≤ Q ≤ 200000$
• $S_{i,j}$ is either $0$ or $1$.
• $S_{i,j}$ satisfies the condition explained in the statement.
• $1 ≤ x_{i,1} ≤ x_{i,2} ≤ N(1 ≤ i ≤ Q)$
• $1 ≤ y_{i,1} ≤ y_{i,2} ≤ M(1 ≤ i ≤ Q)$

Sample Input 1

3 4 4
1101
0110
1101
1 1 3 4
1 1 3 1
2 2 3 4
1 2 2 4

Sample Output 1

3
2
2
2

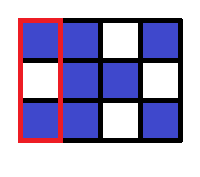
In the first query, the whole grid is specified. There are three components consisting of blue squares, and thus $3$ should be printed.

In the second query, the region within the red frame is specified. There are two components consisting of blue squares, and thus $2$ should be printed. Note that squares that belong to the same component in the original grid may belong to different components.

Sample Input 2

5 5 6
11010
01110
10101
11101
01010
1 1 5 5
1 2 4 5
2 3 3 4
3 3 3 3
3 1 3 5
1 1 3 4

Sample Output 2

3
2
1
1
3
2