Home

Contest: Task: Related: TaskC TaskE

Score : $1600$ points

Problem Statement

There is a rectangle in the $xy$-plane, with its lower left corner at $(0, 0)$ and its upper right corner at $(W, H)$. Each of its sides is parallel to the $x$-axis or $y$-axis. Initially, the whole region within the rectangle is painted white.

Snuke plotted $N$ points into the rectangle. The coordinate of the $i$-th ($1 ≦ i ≦ N$) point was $(x_i, y_i)$.

Then, for each $1 ≦ i ≦ N$, he will paint one of the following four regions black:

  • the region satisfying $x < x_i$ within the rectangle
  • the region satisfying $x > x_i$ within the rectangle
  • the region satisfying $y < y_i$ within the rectangle
  • the region satisfying $y > y_i$ within the rectangle

Find the longest possible perimeter of the white region of a rectangular shape within the rectangle after he finishes painting.

Constraints

  • $1 ≦ W, H ≦ 10^8$
  • $1 ≦ N ≦ 3 \times 10^5$
  • $0 ≦ x_i ≦ W$ ($1 ≦ i ≦ N$)
  • $0 ≦ y_i ≦ H$ ($1 ≦ i ≦ N$)
  • $W$, $H$ (21:32, added), $x_i$ and $y_i$ are integers.
  • If $i ≠ j$, then $x_i ≠ x_j$ and $y_i ≠ y_j$.

Input

The input is given from Standard Input in the following format:

$W$ $H$ $N$
$x_1$ $y_1$
$x_2$ $y_2$
$:$
$x_N$ $y_N$

Output

Print the longest possible perimeter of the white region of a rectangular shape within the rectangle after Snuke finishes painting.

Sample Input 1

10 10 4
1 6
4 1
6 9
9 4

Sample Output 1

32

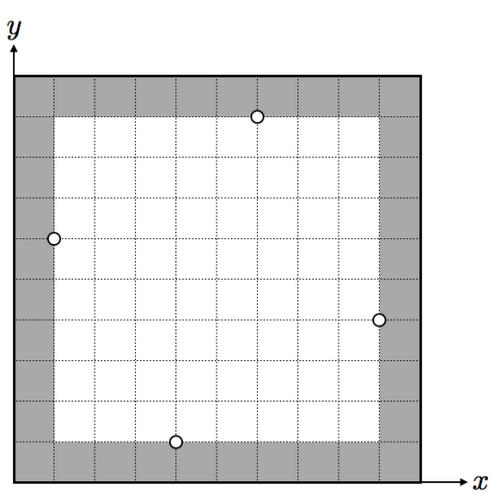
In this case, the maximum perimeter of $32$ can be obtained by painting the rectangle as follows:

842bb3939c9721d978d4e122b0bfff55.png

Sample Input 2

5 4 5
0 0
1 1
2 2
4 3
5 4

Sample Output 2

12

Sample Input 3

100 100 8
19 33
8 10
52 18
94 2
81 36
88 95
67 83
20 71

Sample Output 3

270

Sample Input 4

100000000 100000000 1
3 4

Sample Output 4

399999994