Home

Contest: Task: Related: TaskB TaskD

Score : $1000$ points

Problem Statement

AtCoDeer the deer found $N$ rectangle lying on the table, each with height $1$. If we consider the surface of the desk as a two-dimensional plane, the $i$-th rectangle $i(1≤i≤N)$ covers the vertical range of $[i-1,i]$ and the horizontal range of $[l_i,r_i]$, as shown in the following figure:

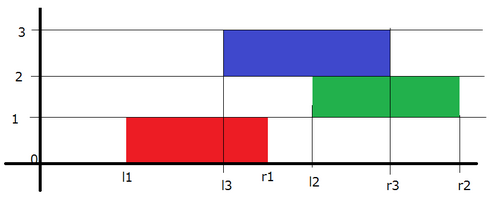
AtCoDeer will move these rectangles horizontally so that all the rectangles are connected. For each rectangle, the cost to move it horizontally by a distance of $x$, is $x$. Find the minimum cost to achieve connectivity. It can be proved that this value is always an integer under the constraints of the problem.

Constraints

All input values are integers.
$1≤N≤10^5$
$1≤l_i<r_i≤10^9$

Partial Score

$300$ points will be awarded for passing the test set satisfying $1≤N≤400$ and $1≤l_i<r_i≤400$.

Input

The input is given from Standard Input in the following format:

$N$
$l_1$ $r_1$
$l_2$ $r_2$
:
$l_N$ $r_N$

Output

Print the minimum cost to achieve connectivity.

Sample Input 1

Sample Output 1

The second rectangle should be moved to the left by a distance of $2$.

Sample Input 2

Sample Output 2

The rectangles are already connected, and thus no move is needed.

Sample Input 3

5
999999999 1000000000
1 2
314 315
500000 500001
999999999 1000000000

Sample Output 3

1999999680

Sample Input 4

5
123456 789012
123 456
12 345678901
123456 789012
1 23

Sample Output 4

Sample Input 5

1
1 400