Home
Contest: Task: Related: TaskB TaskD
Score : $900$ points
Problem Statement
Alice lives on a line. Today, she will travel to some place in a mysterious vehicle. Initially, the distance between Alice and her destination is $D$. When she input a number $x$ to the vehicle, it will travel in the direction of the destination by a distance of $x$ if this move would shorten the distance between the vehicle and the destination, and it will stay at its position otherwise. Note that the vehicle may go past the destination when the distance between the vehicle and the destination is less than $x$.
Alice made a list of $N$ numbers. The $i$-th number in this list is $d_i$. She will insert these numbers to the vehicle one by one.
However, a mischievous witch appeared. She is thinking of rewriting one number in the list so that Alice will not reach the destination after $N$ moves.
She has $Q$ plans to do this, as follows:
- Rewrite only the $q_i$-th number in the list with some integer so that Alice will not reach the destination.
Write a program to determine whether each plan is feasible.
Constraints
- $1≤ N ≤ 5*10^5$
- $1≤ Q ≤ 5*10^5$
- $1≤ D ≤ 10^9$
- $1≤ d_i ≤ 10^9(1≤i≤N)$
- $1≤ q_i ≤ N(1≤i≤Q)$
- D and each $d_i$ are integers.
Input
Input is given from Standard Input in the following format:
$N$ $D$ $d_1$ $d_2$ $...$ $d_N$ $Q$ $q_1$ $q_2$ $...$ $q_Q$
Output
Print $Q$ lines. The $i$-th line should contain YES if the $i$-th plan is feasible, and NO otherwise.
Sample Input 1
4 10 3 4 3 3 2 4 3
Sample Output 1
NO YES
For the first plan, Alice will already arrive at the destination by the first three moves, and therefore the answer is NO.
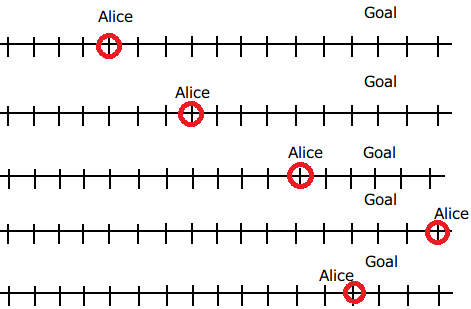
For the second plan, rewriting the third number in the list with $5$ will prevent Alice from reaching the destination as shown in the following figure, and thus the answer is YES.
Sample Input 2
5 9 4 4 2 3 2 5 1 4 2 3 5
Sample Output 2
YES YES YES YES YES
Alice will not reach the destination as it is, and therefore all the plans are feasible.
Sample Input 3
6 15 4 3 5 4 2 1 6 1 2 3 4 5 6
Sample Output 3
NO NO YES NO NO YES