Home
Contest: Task: Related: TaskB TaskD
Score : $700$ points
Problem Statement
Snuke is playing a puzzle game. In this game, you are given a rectangular board of dimensions $R × C$, filled with numbers. Each integer $i$ from $1$ through $N$ is written twice, at the coordinates $(x_{i,1},y_{i,1})$ and $(x_{i,2},y_{i,2})$.
The objective is to draw a curve connecting the pair of points where the same integer is written, for every integer from $1$ through $N$. Here, the curves may not go outside the board or cross each other.
Determine whether this is possible.
Constraints
- $1 ≤ R,C ≤ 10^8$
- $1 ≤ N ≤ 10^5$
- $0 ≤ x_{i,1},x_{i,2} ≤ R(1 ≤ i ≤ N)$
- $0 ≤ y_{i,1},y_{i,2} ≤ C(1 ≤ i ≤ N)$
- All given points are distinct.
- All input values are integers.
Input
Input is given from Standard Input in the following format:
$R$ $C$ $N$
$x_{1,1}$ $y_{1,1}$ $x_{1,2}$ $y_{1,2}$
:
$x_{N,1}$ $y_{N,1}$ $x_{N,2}$ $y_{N,2}$
Output
Print YES if the objective is achievable; print NO otherwise.
Sample Input 1
4 2 3 0 1 3 1 1 1 4 1 2 0 2 2
Sample Output 1
YES
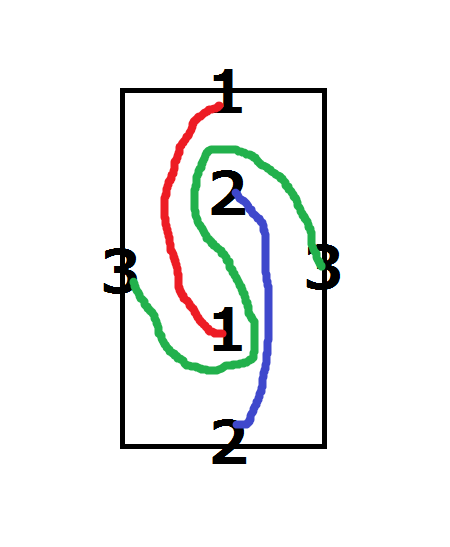
The above figure shows a possible solution.
Sample Input 2
2 2 4 0 0 2 2 2 0 0 1 0 2 1 2 1 1 2 1
Sample Output 2
NO
Sample Input 3
5 5 7 0 0 2 4 2 3 4 5 3 5 5 2 5 5 5 4 0 3 5 1 2 2 4 4 0 5 4 1
Sample Output 3
YES
Sample Input 4
1 1 2 0 0 1 1 1 0 0 1
Sample Output 4
NO