Home

Contest: Task: Related: TaskA TaskC

Score : $500$ points

Problem Statement

You are given two integers $A$ and $B$.

Print a grid where each square is painted white or black that satisfies the following conditions, in the format specified in Output section:

  • Let the size of the grid be $h \times w$ ($h$ vertical, $w$ horizontal). Both $h$ and $w$ are at most $100$.
  • The set of the squares painted white is divided into exactly $A$ connected components.
  • The set of the squares painted black is divided into exactly $B$ connected components.

It can be proved that there always exist one or more solutions under the conditions specified in Constraints section. If there are multiple solutions, any of them may be printed.

Notes

Two squares painted white, $c_1$ and $c_2$, are called connected when the square $c_2$ can be reached from the square $c_1$ passing only white squares by repeatedly moving up, down, left or right to an adjacent square.

A set of squares painted white, $S$, forms a connected component when the following conditions are met:

  • Any two squares in $S$ are connected.
  • No pair of a square painted white that is not included in $S$ and a square included in $S$ is connected.

A connected component of squares painted black is defined similarly.

Constraints

  • $1 \leq A \leq 500$
  • $1 \leq B \leq 500$

Input

Input is given from Standard Input in the following format:

$A$ $B$

Output

Output should be in the following format:

  • In the first line, print integers $h$ and $w$ representing the size of the grid you constructed, with a space in between.
  • Then, print $h$ more lines. The $i$-th ($1 \leq i \leq h$) of these lines should contain a string $s_i$ as follows:
    • If the square at the $i$-th row and $j$-th column ($1 \leq j \leq w$) in the grid is painted white, the $j$-th character in $s_i$ should be ..
    • If the square at the $i$-th row and $j$-th column ($1 \leq j \leq w$) in the grid is painted black, the $j$-th character in $s_i$ should be #.

Sample Input 1

2 3

Sample Output 1

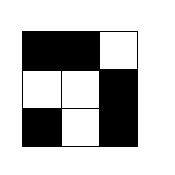
3 3
##.
..#
#.#

This output corresponds to the grid below:

2701558bf42f7c088abad927b419472a.png

Sample Input 2

7 8

Sample Output 2

3 5
#.#.#
.#.#.
#.#.#

Sample Input 3

1 1

Sample Output 3

4 2
..
#.
##
##

Sample Input 4

3 14

Sample Output 4

8 18
..................
..................
....##.......####.
....#.#.....#.....
...#...#....#.....
..#.###.#...#.....
.#.......#..#.....
#.........#..####.