Home
Contest: Task: Related: TaskD TaskF
Score : $1400$ points
Problem Statement
Sigma and Sugim are playing a game.
The game is played on a graph with $N$ vertices numbered $1$ through $N$. The graph has $N-1$ red edges and $N-1$ blue edges, and the $N-1$ edges in each color forms a tree. The red edges are represented by pairs of integers $(a_i, b_i)$, and the blue edges are represented by pairs of integers $(c_i, d_i)$.
Each player has his own piece. Initially, Sigma's piece is at vertex $X$, and Sugim's piece is at vertex $Y$.
The game is played in turns, where turns are numbered starting from turn $1$. Sigma takes turns $1, 3, 5, ...$, and Sugim takes turns $2, 4, 6, ...$.
In each turn, the current player either moves his piece, or does nothing. Here, Sigma can only move his piece to a vertex that is directly connected to the current vertex by a red edge. Similarly, Sugim can only move his piece to a vertex that is directly connected to the current vertex by a blue edge.
When the two pieces come to the same vertex, the game ends immediately. If the game ends just after the operation in turn $i$, let $i$ be the total number of turns in the game.
Sigma's objective is to make the total number of turns as large as possible, while Sugim's objective is to make it as small as possible.
Determine whether the game will end in a finite number of turns, assuming both players plays optimally to achieve their respective objectives. If the answer is positive, find the number of turns in the game.
Constraints
- $2 ≦ N ≦ 200,000$
- $1 ≦ X, Y ≦ N$
- $X \neq Y$
- $1 ≦ a_i, b_i, c_i, d_i ≦ N$
- The $N-1$ edges in each color (red and blue) forms a tree.
Input
The input is given from Standard Input in the following format:
$N$ $X$ $Y$
$a_1$ $b_1$
$a_2$ $b_2$
$:$
$a_{N-1}$ $b_{N-1}$
$c_1$ $d_1$
$c_2$ $d_2$
$:$
$c_{N-1}$ $d_{N-1}$
Output
If the game will end in a finite number of turns, print the number of turns.
Otherwise, print -1.
Sample Input 1
4 1 2 1 2 1 3 1 4 2 1 2 3 1 4
Sample Output 1
4
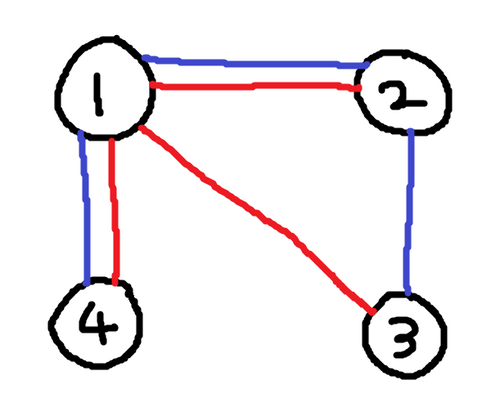
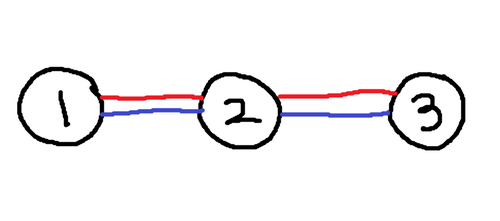
Sample Input 2
3 3 1 1 2 2 3 1 2 2 3
Sample Output 2
4
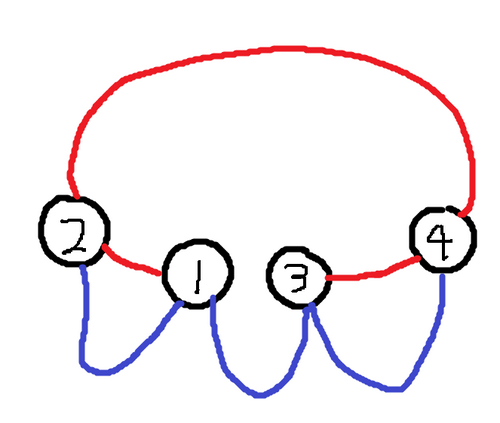
Sample Input 3
4 1 2 1 2 3 4 2 4 1 2 3 4 1 3
Sample Output 3
2
Sample Input 4
4 2 1 1 2 3 4 2 4 1 2 3 4 1 3
Sample Output 4
-1
Sample Input 5
5 1 2 1 2 1 3 1 4 4 5 2 1 1 3 1 5 5 4
Sample Output 5
6