Home

Contest: Task: Related: TaskE TaskG

Score : $1900$ points

Problem Statement

One day, Takahashi was given the following problem from Aoki:

You are given a tree with $N$ vertices and an integer $K$. The vertices are numbered $1$ through $N$. The edges are represented by pairs of integers $(a_i, b_i)$.
For a set $S$ of vertices in the tree, let $f(S)$ be the minimum number of the vertices in a subtree of the given tree that contains all vertices in $S$.
There are 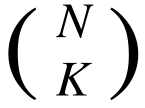ways to choose $K$ vertices from the trees. For each of them, let $S$ be the set of the chosen vertices, and find the sum of $f(S)$ over all 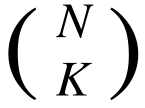ways.
Since the answer may be extremely large, print it modulo $924844033$(prime).

Since it was too easy for him, he decided to solve this problem for all $K = 1,2,...,N$.

Constraints

$2 ≦ N ≦ 200,000$
$1 ≦ a_i, b_i ≦ N$
The given graph is a tree.

Input

The input is given from Standard Input in the following format:

$N$
$a_1$ $b_1$
$a_2$ $b_2$
$:$
$a_{N-1}$ $b_{N-1}$

Output

Print $N$ lines. The $i$-th line should contain the answer to the problem where $K=i$, modulo $924844033$.

Sample Input 1

3
1 2
2 3

Sample Output 1

3
7
3

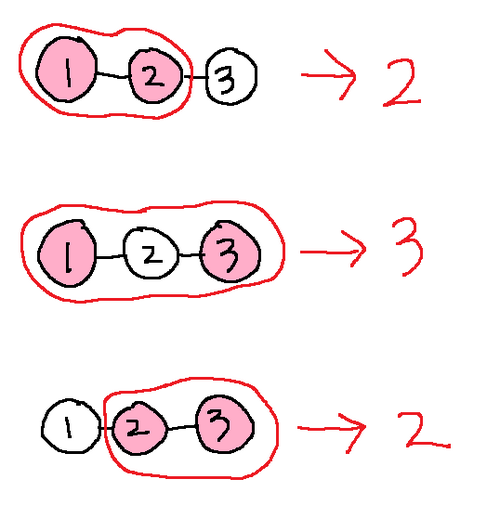
The diagram above illustrates the case where $K=2$. The chosen vertices are colored pink, and the subtrees with the minimum number of vertices are enclosed by red lines.

Sample Input 2

Sample Output 2

Sample Input 3

Sample Output 3