Home

Contest: Task: Related: TaskB TaskD

Score : $700$ points

Problem Statement

You are given four integers: $H$, $W$, $h$ and $w$ ($1 ≤ h ≤ H$, $1 ≤ w ≤ W$). Determine whether there exists a matrix such that all of the following conditions are held, and construct one such matrix if the answer is positive:

  • The matrix has $H$ rows and $W$ columns.
  • Each element of the matrix is an integer between $-10^9$ and $10^9$ (inclusive).
  • The sum of all the elements of the matrix is positive.
  • The sum of all the elements within every subrectangle with $h$ rows and $w$ columns in the matrix is negative.

Constraints

  • $1 ≤ h ≤ H ≤ 500$
  • $1 ≤ w ≤ W ≤ 500$

Input

Input is given from Standard Input in the following format:

$H$ $W$ $h$ $w$

Output

If there does not exist a matrix that satisfies all of the conditions, print No.

Otherwise, print Yes in the first line, and print a matrix in the subsequent lines in the following format:

$a_{11}$ $...$ $a_{1W}$
$:$
$a_{H1}$ $...$ $a_{HW}$

Here, $a_{ij}$ represents the $(i,\ j)$ element of the matrix.

Sample Input 1

3 3 2 2

Sample Output 1

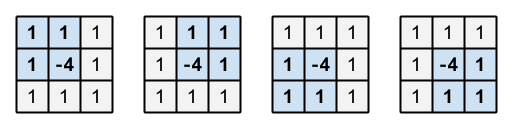
Yes
1 1 1
1 -4 1
1 1 1

The sum of all the elements of this matrix is $4$, which is positive. Also, in this matrix, there are four subrectangles with $2$ rows and $2$ columns as shown below. For each of them, the sum of all the elements inside is $-1$, which is negative.

bbdb651fa1f05996886da9f0c4d8090a.png

Sample Input 2

2 4 1 2

Sample Output 2

No

Sample Input 3

3 4 2 3

Sample Output 3

Yes
2 -5 8 7
3 -5 -4 -5
2 1 -1 7