Home
Contest: Task: Related: TaskD TaskF
Score : $1200$ points
Problem Statement
We have $N$ irregular jigsaw pieces. Each piece is composed of three rectangular parts of width $1$ and various heights joined together. More specifically:
- The $i$-th piece is a part of height $H$, with another part of height $A_i$ joined to the left, and yet another part of height $B_i$ joined to the right, as shown below. Here, the bottom sides of the left and right parts are respectively at $C_i$ and $D_i$ units length above the bottom side of the center part.
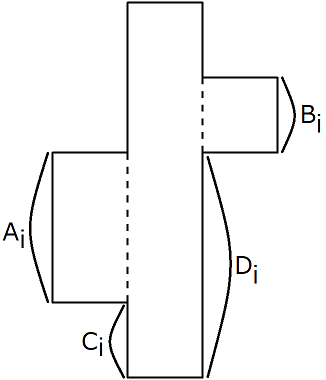
Snuke is arranging these pieces on a square table of side $10^{100}$. Here, the following conditions must be held:
- All pieces must be put on the table.
- The entire bottom side of the center part of each piece must touch the front side of the table.
- The entire bottom side of the non-center parts of each piece must either touch the front side of the table, or touch the top side of a part of some other piece.
- The pieces must not be rotated or flipped.
Determine whether such an arrangement is possible.
Constraints
- $1 \leq N \leq 100000$
- $1 \leq H \leq 200$
- $1 \leq A_i \leq H$
- $1 \leq B_i \leq H$
- $0 \leq C_i \leq H - A_i$
- $0 \leq D_i \leq H - B_i$
- All input values are integers.
Input
Input is given from Standard Input in the following format:
$N$ $H$ $A_1$ $B_1$ $C_1$ $D_1$ $A_2$ $B_2$ $C_2$ $D_2$ : $A_N$ $B_N$ $C_N$ $D_N$
Output
If it is possible to arrange the pieces under the conditions, print YES; if it is impossible, print NO.
Sample Input 1
3 4 1 1 0 0 2 2 0 1 3 3 1 0
Sample Output 1
YES
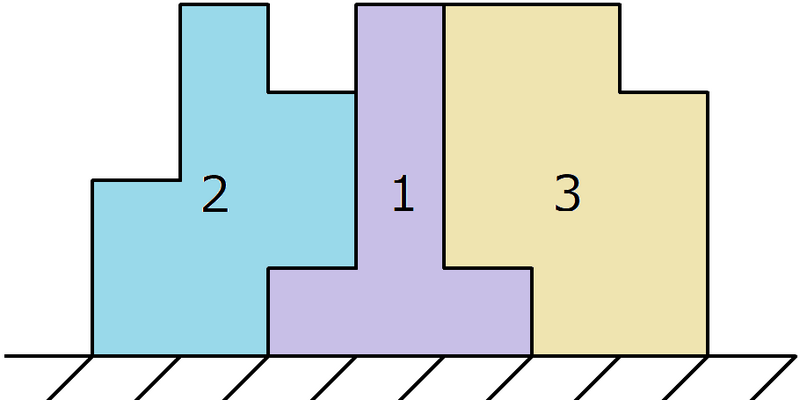
The figure below shows a possible arrangement.
Sample Input 2
4 2 1 1 0 1 1 1 0 1 1 1 0 1 1 1 0 1
Sample Output 2
NO
Sample Input 3
10 4 1 1 0 3 2 3 2 0 1 2 3 0 2 1 0 0 3 2 0 2 1 1 3 0 3 2 0 0 1 3 2 0 1 1 1 3 2 3 0 0
Sample Output 3
YES