Home
Contest: Task: Related: TaskE TaskG
Score : $1600$ points
Problem Statement
There are $N(N+1)/2$ dots arranged to form an equilateral triangle whose sides consist of $N$ dots, as shown below. The $j$-th dot from the left in the $i$-th row from the top is denoted by $(i, j)$ ($1 \leq i \leq N$, $1 \leq j \leq i$). Also, we will call $(i+1, j)$ immediately lower-left to $(i, j)$, and $(i+1, j+1)$ immediately lower-right to $(i, j)$.
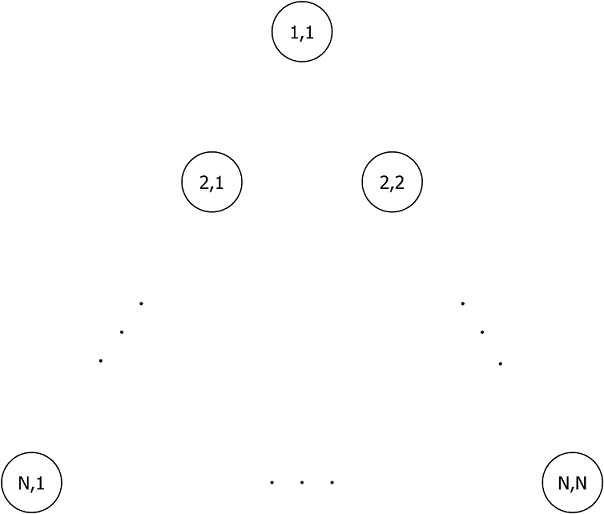
Takahashi is drawing $M$ polygonal lines $L_1, L_2, ..., L_M$ by connecting these dots. Each $L_i$ starts at $(1, 1)$, and visits the dot that is immediately lower-left or lower-right to the current dots $N-1$ times. More formally, there exist $X_{i,1}, ..., X_{i,N}$ such that:
- $L_i$ connects the $N$ points $(1, X_{i,1}), (2, X_{i,2}), ..., (N, X_{i,N})$, in this order.
- For each $j=1, 2, ..., N-1$, either $X_{i,j+1} = X_{i,j}$ or $X_{i,j+1} = X_{i,j}+1$ holds.
Takahashi would like to draw these lines so that no part of $L_{i+1}$ is to the left of $L_{i}$. That is, for each $j=1, 2, ..., N$, $X_{1,j} \leq X_{2,j} \leq ... \leq X_{M,j}$ must hold.
Additionally, there are $K$ conditions on the shape of the lines that must be followed. The $i$-th condition is denoted by $(A_i, B_i, C_i)$, which means:
- If $C_i=0$, $L_{A_i}$ must visit the immediately lower-left dot for the $B_i$-th move.
- If $C_i=1$, $L_{A_i}$ must visit the immediately lower-right dot for the $B_i$-th move.
That is, $X_{A_i, {B_i}+1} = X_{A_i, B_i} + C_i$ must hold.
In how many ways can Takahashi draw $M$ polygonal lines? Find the count modulo $1000000007$.
Notes
Before submission, it is strongly recommended to measure the execution time of your code using "Custom Test".
Constraints
- $1 \leq N \leq 20$
- $1 \leq M \leq 20$
- $0 \leq K \leq (N-1)M$
- $1 \leq A_i \leq M$
- $1 \leq B_i \leq N-1$
- $C_i = 0$ or $1$
- No pair appears more than once as $(A_i, B_i)$.
Input
Input is given from Standard Input in the following format:
$N$ $M$ $K$ $A_1$ $B_1$ $C_1$ $A_2$ $B_2$ $C_2$ : $A_K$ $B_K$ $C_K$
Output
Print the number of ways for Takahashi to draw $M$ polygonal lines, modulo $1000000007$.
Sample Input 1
3 2 1 1 2 0
Sample Output 1
6
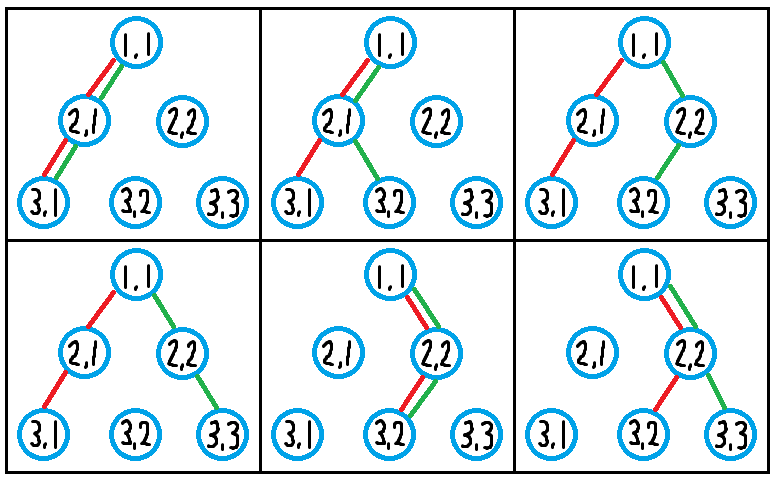
There are six ways to draw lines, as shown below. Here, red lines represent $L_1$, and green lines represent $L_2$.
Sample Input 2
3 2 2 1 1 1 2 1 0
Sample Output 2
0
Sample Input 3
5 4 2 1 3 1 4 2 0
Sample Output 3
172
Sample Input 4
20 20 0
Sample Output 4
881396682